Nearly a third of a century ago, on a tropical island in the South Pacific far, far away, I started organizing weekly educational and public StarWatches as the laboratory portion for a high school astronomy class. The astronomy class was designed around scientist and science popularizer, Carl Sagan’s PBS produced 13-part, award-winning and ground-breaking television citizen science series, “Cosmos,” originally broadcast in late 1980.
The 13-part series Cosmos was seen by an estimated 500 million people in 60 countries — when the total world population was 4.5 billion. One out of nine people living on planet Earth in 1980 watched the Cosmos series. The class textbook would be Carl Sagan’s best-selling book “Cosmos” based upon and expanding the content of the PBS mini-series. Each of the 13-hour-long Cosmos videos offered visualizations and videos that were translated into a chapter of the book by the same name.

I was not the original inventor of formal and informal public telescopic astronomy education. That lofty title probably goes to the Italian scientist, astronomer and inventor Galileo Galilei three and three-quarters centuries before my contributions. My personal input into the legacy of the StarWatch was to create a working format of educational and public StarWatches that met the needs of my students, their families and friends on the island of Tutuila, American Samoa. My students and their families were the direct descendants of a proud and noble seafaring people that explored, colonized and traded across the entire vast Pacific Ocean that spans nearly half the surface of our planet! The stars helped to guide the ancestors of my students across the open ocean and to find their way back to small islands far over the horizon. I wanted to tap into and reignite this nearly lost local resource little used for centuries.
Beyond the text and video of Sagan’s Cosmos, the astronomy class would use planetarium software designed for the Apple IIe computer to show what was in the night sky. The computer software displayed constellations, moon phases and the orbital orientation of the four largest moons of the planet Jupiter. One of the unexpected lessons learned was the utter amazement of the students in comparing the computer modeling via the planetarium software of the night sky constellations, phases of the moon and the orientation of Jupiter’s four largest moons compared directly to their first-hand observations at the weekly StarWatch laboratories. The universe, they found, could be both modeled and highly predictable.
Added to this mix was the idea of using telescopes from the now-defunct Coulter Optical Co. An advertisement in Astronomy Magazine offered an 8-inch (20 cm) reflector telescope (using a parabolic mirror at the back of the telescope rather than a glass lens in the front). The ad stated that the 8-inch reflector telescope cost only $235, and shipping was free anywhere in the U.S. — hmmm. Coulter Optical was an American company, so it made sense that shipping to any one of the 50 states would be the same, however, I was in American Samoa, one of the five U.S. Territories (with 11 additional minor outlying islands).
My reasoning was this: Hawaii was a remote U.S. state and yet there was no, “except for Hawaii” in the ad. American Samoa was a remote U.S. Territory. What if Coulter Optical could send me an 8-inch telescope? Additionally, the ad mentioned a 17.5-inch (44.5 cm) reflector telescope for the low, low price of only $995!!! I did the math: the “Light Gathering Power” of a telescope was directly related to the “area” of the mirror. A 17.5-inch mirror has more than 4.8 times the area of the mirror in an 8-inch telescope — a 17.5-inch telescope could thus see fainter celestial objects and further into space! A larger telescope mirror has an additional bonus: the “Resolving Power” of a telescope is a telescope’s ability to clearly separate two close stars, lunar features or planetary details. Resolving Power for telescopes of this size is directly related to the diameter of the primary mirror. A 17.5-inch telescope would reveal 2.2 times the detail on the lunar surface, planets and star-fields while making these sky objects 4.8 times brighter than in an 8-inch telescope. The cost of this 17.5-inch monster was seven percent of my annual salary. … However, I was living in American Samoa, in the middle of the South Pacific Ocean, with very little light pollution. The village of Leone on the southwestern end of Tutuila island was 14.34 degrees below the equator!
From this unique vantage point could be viewed dark southern sky gems hidden from the sky observers in the northern hemisphere. Any clear moonless night in American Samoa, while school is in session, shows the star clouds of Magellan, nearby (galactically speaking) satellite galaxies, small galactic neighbors orbiting our larger home galaxy, the Milky Way Galaxy. The Large and Small Magellanic Clouds were easily visible to the unaided eye like rogue chunks of the Milky Way set loose into the sky. Imagine the wondrous sights freed to my student’s eyes, gazing into the Clouds of Magellan with an 8-inch telescope? What distant galactic treasures in space and time would be revealed to my students using a 17.5-inch telescope? My mind swam with the possibilities. Having a telescope would seal the fate of my proposed astronomy class. Getting a telescope was the key. With no telescope, the proposed astronomy class would be at best a mere “science-based elective class” and not likely to be granted. A telescope would make the proposed astronomy class a “laboratory-based science class” qualifying it as a full-fledged science class that would satisfy requirements for science credit to be used toward graduation.

The more I thought about a 17.5-inch telescope and the southern sky celestial phenomena it would unseal, the more excited I became. Open star clusters, galaxies and the mysterious globular star clusters (the Samoan sky had the two best). The constellation of Sagittarius (full of numerous nebula and star clusters) in the direction of the core of the Milky Way Galaxy was high in the skies of the Samoan winter. In the skies of East and West Virginia, the glory of Sagittarius is muted, low in the haze of the southern summer skies.
It was settled. I would contact the Coulter Optical Co. and order a 17.5-inch telescope. It would cost the better part of $1,000, but, I would get to teach the astronomy class in American Samoa.
The ad included a phone number. Having no phone, I asked a neighbor if I could use his phone and pay him for the overseas phone call. The folks at Coulter Optical were courteous and pleasant. They had never received an order from American Samoa. The 17.5-inch telescope would need to be shipped via, well, a ship, and would take several to six months to arrive. I would have to pay the shipping, adding another third of the cost of the telescope (more than 10 percent of my annual salary). However, an 8-inch telescope could be in American Samoa in six weeks, and they would pay for the shipping. I had my heart set on the 17.5-inch monster telescope, but it was not going to get to Samoa in time to start the astronomy class. I thanked the Coulter Optical rep and hung up.
My neighbor asked, “So we are not going to get to look through the giant telescope?”
“Sorry,” I said.
“Why not?”
“Well …”
I thought about it and said, “Can I use your phone again?”
I called Coulter Optical back quickly and ordered both telescopes. We would start with the 8-inch telescope and then when we thought the objects in the night sky could not get any better, along will come the 17.5-inch monster — I swore my neighbor to secrecy. He agreed, as long as he got to be first to look through it.

I was able to start the astronomy class with the 8-inch telescope for Friday Night StarWatch Labs. I scheduled the first Laboratory StarWatch with the moon in the sky. The Earth’s moon as seen through a telescope reveals a remarkably tangible world with some recognizable large-scale features we see on our own world, and some we are not closely aquainted with.

The first student to look through the 8-inch telescope at the moon during the first StarWatch paused … after a few seconds he said, “Where are they, I don’t see ’em?”
I thought he meant the craters and the mountain ranges. Did the telescope get bumped? He continued, “Where are the footprints of the astronauts? And where is the flag?”
It would not be a piece of fictional exaggeration to say that this essential astronomical question has been posed to me more than a thousand times at various StarWatches over nearly a third of a century. Stargazers looking at the lunar surface with the magnification and light gathering powers of a telescope frequently ask: “Can you see the footprints/flag/rover from the Apollo astronaut landings?”

I usually respond, “The moon is actually very big and very far away, and the footprints, flag, rover, etc. are just too small to see even using a telescope.”
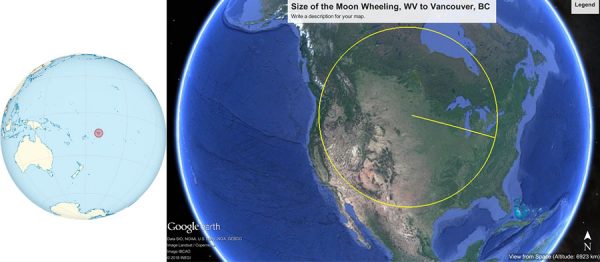
How big is the Earth’s moon? The average diameter of the moon and its magnified image floating in the eyepiece of a telescope is 3,474.2 km (2,158.8 miles) across. This is about the distance from Leone, American Samoa, to nearly Christchurch, New Zealand … or Wheeling, W.Va, to Vancouver, B.C., Canada. Imagine looking at this huge expansive distance of the moon and looking for something as small as a house, a car, a dog or a footprint? These objects would be way, way too small to see simply because the moon is so vastly big and so very far away.
Let’s address a common misconception concerning the ratio of the diameters of the Earth’s large natural satellite, the moon and Earth (assume both worlds are spherical for the following discussion). Many science texts share the misconception that the ratio of the sizes of the diameter of the moon and Earth is equal to 1 to 4. Meaning that the diameter of the moon is 25 percent, one quarter, one fourth, 0.25, 1/4, of the diameter of the Earth. Doing the mathematics of the ratios of the average diameters of the moon to the Earth in miles (2,158.8 miles)/(7,919.0 miles), the units, miles/miles cancel out to 1, leaving a simple numerical ratio of 0.27261. This answer 0.27261 is close to 0.25, but the math here is a bit off, a little sloppy. How sloppy? We can use the “% Error” method to find out:
The percentage error here is found to equal the Absolute Value of {(0.25000) — (0.27261)} divided by {(0.27261)} = 0.082939 x 100 = 8.3 % Error. If we use 0.25 as the ratio of the diameters of the moon and the Earth, this is in error by 8.3 percent or about one part in 12. My personal threshold for letting any “mathematical rounding” be close enough to be used as a sound-bite or rule of thumb is 5 percent.

Can we use a simple ratio other than 1/4 that is closer and be more exact? Of course, a little math playing with a calculator, soon shows that a ratio of 3/11 is equal to 0.272727… (and keeps going as a repeating decimal) we will round off this number to 0.27273. Why then do our textbooks use the ratio 1/4 to relate the size of the moon in terms of the size of the Earth?
My theory is simple: mathematical laziness. We humans are hard-wired and pre-programmed to recognize simple fractions like 1/2 or 1/3 or 2/3, (hmmm — sounds like a future topic for this article series). Note: that the fraction ratio 1/4 is really the same as a half of a half. Humans are then also hard-wired and pre-programmed to recognize the fractions or ratios: 1/4, 2/4 and 3/4. Humans think in simple fractions, it is easy for us. We humans do not easily think in ratios of 11ths, and the universe spends zero effort in trying to make “random numerical ratio outcomes” easier for humans to think about. It is not for our personal ease that we need to think about the diameter ratios of the moon to the Earth as closer to 3/11 than 1/4, it is in simple fact closer to the truth. The ratio 3/11 is a truer truth. Using the “% Error” method, we can find out how close the estimate of 3/11 is to the actual ratio of the average diameters of the moon to the Earth. Let’s use the “% Error” method to see how close 3/11 is to the real moon/Earth ratio:
Absolute Value of {(0.27273) — (0.27261)} divided by {(0.27261)} = 0.00044019 x 100 = 0.044 % Error. The % Error in using 3/11 as the ratio of the diameters of the moon and Earth is only about 44/1000 of a percent in error, or one part in 2,273 (189 times better than 0.25) … I can mathematically live with this level of rounding off.
Look for Part II, “Why Can’t We See the Footprints on the Moon?” during the full moon this “Moonth”
I hope that you gentle readers will take the time to contact me Robert@smartcenter.org and let me know if there is a science topic you would like me to cover in this “Moonthly,” every Lunar 1st Quarter, science column. In the subject heading please type in the phrase “A View from the Moon” and the date. I look forward to a long and fruitful partnership with you, the gentle readers of Weelunk.
• Robert E. Strong received a bachelor of arts degree in physics with minors in mathematics and philosophy and has a master’s degree in space studies. Robert taught secondary school math and science in Benin, West Africa, (Peace Corps volunteer) and in American Samoa. He worked as a physicist in a research laboratory. Robert is president of the Near Earth Object Foundation dedicated to educating the general public about Near Earth Objects and providing public StarWatches. Robert and his wife Libby started the SMART-Center in 1994, a hub for science- and math-related activities for area schools, educators and the community. They also operate the SMART Centre Market — an interactive hands-on science store in Wheeling, featuring Orion telescopes, science toys and Kirke’s ice cream.




